Searching

list : 하나 이상의 필드로 된 레코드의 집합
키 (key) : 레코드를 구분하기 위해서 사용되는 필드
순차 탐색(Sequential Search)
- 레코드 리스트를 왼편에서 오른편 또는 오른편에서 왼편으로 레코드를 검사하는 것
- int SeqSearch(int a[], const int n, const int key) { for (int i = 1; i <= n && a[i] != k; i++); if (i > n) return 0; return i; }
이원 탐색 (Binary Search)
- n개의 레코드를 가진 리스트를 탐색하기 위해 O(logn) 시간이 걸림 (순차탐색보다 빠르다.)
  순차나 이원 탐색 방법은 실제로 사람이 사용하는 탐색 방법과 대응되지 않는다.
보간법(interpolation)에 의한 탐색
- 리스트가 정렬되었을 때만 사용 가능
- 탐색의 성질은 리스트에 있는 키의 분포에 달려있음

리스트를 반복해서 탐색할 때, 리스트를 정렬된 상태로 유지하는 것이 이롭다.

Sorting

정렬의 필요성

탐색에서 보조로 사용
리스트의 엔트리를 비교하는 방법으로 사용
정렬 방법
- 내부 방법 (internal method) : 정렬할 리스트가 작아서 전체적인 정렬이 메인 메모리 상에서 실행될 수 있을 때 사용
- 외부 방법 (external method) : 큰 리스트에 사용

정렬 방법

Bubble sort (exchange)

void BubbleSort() { // 맨 뒤에서부터 정렬된다.
	for (int i = 0; i < 10; i++) {
		for (int j = 9; j >= i + 1; j--) {
			if (arr[j] < arr[j - 1]) {
				swap(arr[j], arr[j - 1]);
			}
		}
	}
}

Insertion sort

void InsertionSort() {
	int i, j;
	for (i = 1; i < 10; i++) {
		int key = arr[i];
		for (j = i - 1; j >= 0 && arr[j] > key; j--) {
			arr[j + 1] = arr[j];
		}
		arr[j + 1] = key;
	}
}

Selection sort

void SelectionSort() {
	for (int i = 0; i < 9; i++) {
		int smallest = i;
		for (int j = i + 1; j < 10; j++) {
			if (arr[smallest] > arr[j]) {
				smallest = j;
			}
		}
		swap(arr[i], arr[smallest]);
	}
}

$ N^2 $ 알고리즘의 비교

삽입 정렬은 교환정렬 보다는 항상 최소한 빠르게 수행된다고 할 수 있다.
선택정렬이 교환정렬보다 빠른가? - 일반적으로는 선택정렬 알고리즘이 빠르다고 할 수 있다. 그러나 입력이 이미 정렬되어 있는 경우, 선택정렬은 지정이 이루어지지만 교환정렬은 지정이 이루어지지 않으므로 교환정렬이 빠르다
선택정렬 알고리즘이 삽입정렬 알고리즘보다 빠른가? - n의 크기가 크고, 키의 크기가 큰 자료구조 일 때는 지정하는 시간이 많이 걸리므로 선택정렬 알고리즘이 더 빠르다.

Quick sort
- 시간복잡도 : 파티션 O(n) , 분할 O(logn)
- 힙정렬과 같다.
- 적은 비교
- 이미 거의 정렬이 되어 있을 경우에는 파티션이 고르게 분배하지 못하기 때문에 최악의 경우 O(n^2)의 시간복잡도를 가진다.

void QuickSort(int start, int end) {
    if (start >= end)
        return;
    int pivot = arr[start];
    int left = start + 1;
    int right = end;

    while (left <= right) {
        while (left <= end && arr[left] <= pivot) {
            left++;
        }
        while (right > start && arr[right] >= pivot) {
            right--;
        }
        if (left < right) {
            swap(arr[left], arr[right]);
        }
    }
    swap(arr[start], arr[right]);
    QuickSort(start, right - 1);
    QuickSort(right + 1, end);
}

Merge sort
- 입력 리스트를 길이가 1인 n개의 정렬된 서브리스트로 간주
1. 리스트들을 쌍으로 합병하여 크기가 2인 n/2개의 리스트를 얻는다. (n이 홀수이면 리스트 하나는 크기가 1)
2. n/2개의 리스트를 다시 쌍으로 합병하여 n/4개의 리스트를 얻는다.
3. 합병 단계는 하나의 서브 리스트가 남을 때까지 계속된다. (한 번 합병할 때마다 서브 리스트의 수는 반으로 줄어든다.)
- 시간 복잡도
  - 합병의 각 단계에 걸리는 시간 : O(n)
  - 총 연산 시간 O(nlogn)
- 순환 합병 정렬 : 정렬할 리스트를 거의 똑같이 두 개로 나눈다.
  - 서브리스트들은 순환적으로 정렬된다.
  - 정렬된 서브리스트들은 합병된다.
  - 안정적이다.
  - 연산 시간 O(nlogn)
- 자연 합병 정렬 : 합병 정렬의 변형, 입력 리스트 내에 이미 존재하고 있는 순서를 고려, 이미 정렬되어 있는 레코드의 서브리스트를 식별할 수 있도록 초기 패스를 만들어야함

void Merge(int start, int end, int mid) {
    int i = start, j = mid + 1, k = start, l;

    while (i <= mid && j <= end) {
        if (arr[i] < arr[j]) {
            sorted[k++] = arr[i++];
        } else {
            sorted[k++] = arr[j++];
        }
    }

    while (i <= mid) {
        sorted[k++] = arr[i++];
    }
    while (j <= end) {
        sorted[k++] = arr[j++];
    }

    for (l = start; l <= end; l++) {
        arr[l] = sorted[l];
    }
}



void MergeSort(int start, int end) {

    if (start < end) {
        int mid = (start + end) / 2;
        MergeSort(start, mid); // 분할
        MergeSort(mid + 1, end);
        Merge(start, end, mid); // 정복
    }
}

Heap sort
- 합병 정렬의 문제점 : 정렬한 레코드 수에 비례하여 저장 공간이 추가로 필요하다.
- 일정한 양의 저장공간만 추가로 필요
- 최악의 경우 연산 시간과 평균 연산 시간 : O(nlogn)
  - O(n)의 추가 저장 공간을 사용하는 합병 정렬보다 약간 느리지만 O(1)의 추가 저장 공간을 사용하는 합병 정렬보다 빠름
- 최대-힙 구조 사용
  - 최대힙과 연관된 삭제, 삽입 함수 : O(nlogn)정렬 방법
  - Adjust 함수 사용 - 최대 힙을 재조정

void PushHeap(int seq) {
	if (seq == 1) {
		return;
	}
	while (seq > 0) {
		int parent = seq / 2;
		if (heap[parent] > heap[seq]) {
			swap(heap[parent], heap[seq]);
		} else { break; }
		seq = parent;
	}
}

void PopHeap(int remain) {
	swap(heap[1], heap[remain]);

	int seq = 1;
	while (seq < remain) {
		int left_child = seq * 2;
		int right_child = seq * 2 + 1;
		
		if (left_child >= remain && right_child >= remain) {
			break;
		}
		else if (right_child >= remain) {
			if (heap[left_child] < heap[seq]) {
				swap(heap[left_child], heap[seq]);
			}
			break;
		}

		if (heap[seq] < heap[left_child] && heap[seq] < heap[right_child]) {
			break;
		}
		if (heap[left_child] < heap[right_child]) {
			swap(heap[left_child], heap[seq]);
			seq = left_child;
		} else {
			swap(heap[right_child], heap[seq]);
			seq = right_child;
		}
	}
}

void HeapSort() {
	for (int i = 1; i <= 10; i++) {
		heap[i] = arr[i - 1];
		PushHeap(i);
	}

	int remain = 10;
	for (int i = 0; i < 10; i++) {
		arr[i] = heap[1];
		PopHeap(remain);
		remain--;
	}
}

Radix sort
- 어떤 기수 r을 이용하여 정렬 키를 몇 개의 숫자로 분배 (r = 10 : 십진수, r = 2 : 이진수)
- 기수-r 정렬에서는 r개의 bin이 필요
  - 정렬되어야 하는 레코드가 $ R_1, ... R_n $ 일 때, 레코드의 키는 기수-r을 이용하여 분할 -> 0 ~ (r-1) 사이의 d개의 숫자를 가진 키가 된다.
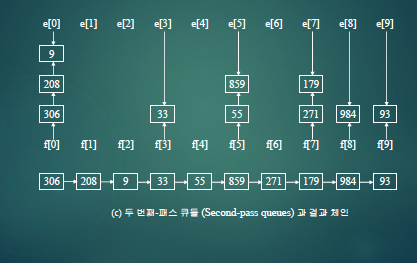
  - 각 빈의 레코드는 빈의 첫 레코드를 가리키는 포인터와 마지막 레코드를 가리키는 포인터를 통해 체인으로 연결되며, 체인은 큐처럼 동작
- 전체 연산 시간 : O(d(n + r))
  - d 패스를 처리하면서 각 패스의 연산 시간은 O(n + r)이다.
- r의 선택을 달리하면 연산 시간이 달라진다.
- 단계별로 알아보자

내부 정렬 요약

내부 정렬 비교
- 삽입 정렬 : 리스트가 부분적으로 정렬되어 있을 때 좋음, 작은 n에 대해 가장 좋은 정렬 방법
- 합병 정렬 : 최악의 경우에 가장 좋은 방법 힙정렬에 비해 더 많은 공간을 필요로 함
- 퀵 정렬 : 평균 성능이 가장 좋음 / 최악의 경우 O(n^2)
- 기수 정렬 : 성능이 키의 크기와 r의 선택에 영향을 받음

퀵 정렬이 적절히 큰 n에 대해 다른 정렬 방법보다 성능이 우수
50과 100사이에 삽입과 퀵 정렬이 분리하는 점
정확한 분리점을 nBreak라고 할 때
- n < nBreak 일 때, 삽입 정렬이 가장 좋은 정렬 방법
- n > nBreak 일 때, 퀵 정렬이 가장 좋은 정렬 방법
- 최악의 경우 n < c에 대해 합병 정렬이 가장 좋게 보여짐
- n <= c 에 대해서는 삽입 정렬이 최악의 경우 가장 좋다.