[C++] 백준 11051 이항계수 2

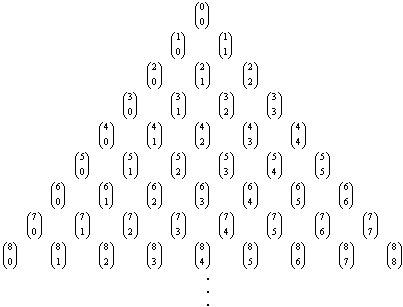
파스칼의 삼각형

이항계수 문제는 조합 공식으로도 풀 수 있으나 파스칼의 삼각형을 이용하면 더 쉽게 답을 얻어낼 수 있다!

삼각형을 그리는 규칙

1. 숫자가 들어갈 칸을 첫 번째 줄에는 1개, 두 번째 줄에는 2개, 세 번째 줄에는 3개 이런 식으로 한 줄씩 내려가면 한 칸씩 늘어나게 정삼각형 모양으로 만든다.
2. 첫 번째 줄과 두 번째 줄의 3칸에는 1을 쓴다.
3. 세 번째 줄부터는 줄의 양쪽 끝 칸에는 1을 쓰고 나머지 칸에는 바로 윗줄에 위치한 칸 중 해당 칸과 인접해 있는 두 칸의 숫자를 더해서 그 값을 쓴다.

위와 아래는 같다.

• n개의 물체에서 r개를 고른다 하자. 먼제 n개중 1개를 고정, A라 한다. 그럼 구하고자 하는 경우의 수는 A가 포함되는 경우와 포함되지 않는 경우 2가지로 나눌 수 있다.

• A가 포함되는 경우 나머지 n - 1개 중 r - 1개를 고르면 되므로 가짓수는

  $$\begin{pmatrix}n - 1\r - 1\ \end{pmatrix}
  $$

• A가 포함되지 않는 경우 나머지 n - 1개 중 r개를 고르면 되므로

  $$\begin{pmatrix}n - 1\r\ \end{pmatrix}
  $$

• 합의 법칙에 의해

  $$\begin{pmatrix}n\r\ \end{pmatrix} = \begin{pmatrix}n - 1\r - 1\ \end{pmatrix} + \begin{pmatrix}n - 1\r\ \end{pmatrix}
  $$

• 이를 통해 점화식을 만들어보면

dp[n][r] = dp[n - 1][[r - 1] + dp[n - 1][[r];

구현

1. dp 배열을 만들고 첫번째, 두번째 줄을 1로 초기화 해준다.
2. 위 점화식을 사용하여 d[n][r]까지 채운다.

• 우리는 10007로 나눈 나머지 값이 필요하므로 나머지 값을 채운다.
• (a + b) % c = (a % c)(b % c) 이기 때문에!

3. 출력한다.

void sol(void)
{
    dp[0][0] = 1;
    dp[1][0] = 1;
    dp[1][1] = 1;

    for (int i = 2; i <= N; i++)
    {
        dp[i][0] = 1;
        dp[i][i] = 1;
    }

    for (int i = 2; i <= N; i++)
    {
        for (int j = 1; j < i && j <= K; j++)
            dp[i][j] = (dp[i - 1][j] + dp[i - 1][j - 1]) % 10007;
    }
    cout << dp[N][K];
}

끝!